Heaps

Binary heap data structure - Has a method heap-size that gives you the number of element from the heap that are in the array, so that $A[i:n]\le A.heapSize\le n$

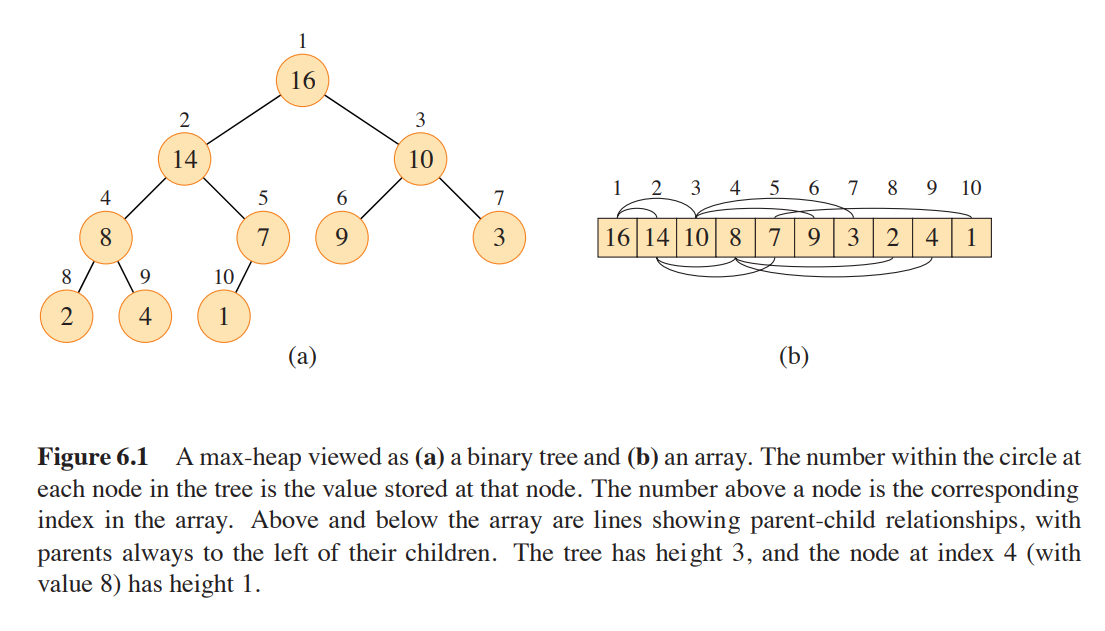
Given the root of a tree is $A[1]$, and you are given the index $i$ of a node, you can calculate the indices of it’s parent, left child, and right child with the following code:

PARENT(i)
	return floor(i/2)

LEFT(i)
	return 2i

RIGHT(i)
	return 2i + 1

Types of Heaps §

There are two types of heaps but each type has a heap priority.

1. Max-Heap - The heap will have a root that is the max number in the heap. The priority is that for every node $i$ other than the root $A[PARENT(i)]\ge A[i]$
   1. HEAP-SORT uses the max-heap!
2. Min-Heap - The heap will have a root that is the min number in the heap. The priority is that for every node $i$ other than the root $A[PARENT(i)]\le A[i]$
   1. Min-heaps area commonly used to implement priority queues.

Time Complexity §

Height of a node - the longest simple downward path from the node to a leaf. The height of a tree is the height from the root node. A heap of n elements has a height of $\Theta (lgn)$ and basic operations on heaps run in time at most proportional to the height of the tree. Thus they take $O(lgn)$ time.

• The MAX-HEAPIFY procedure, which runs in $O(lgn)$ time, is the key to maintaining the max-heap property.
• The BUILD-MAX-HEAP procedure, which runs in linear time, produces a maxheap from an unordered input array.
• The HEAPSORT procedure, which runs in $O(nlgn)$ time, sorts an array in place.
• The procedures MAX-HEAP-INSERT, MAX-HEAP-EXTRACT-MAX, MAXHEAP-INCREASE-KEY, and MAX-HEAP-MAXIMUM allow the heap data structure to implement a priority queue. They run in $O(lgn)$ time plus the time for mapping between objects being inserted into the priority queue and indices in the heap.